I’ve been watching the technology of personal drones improve for years as a casual observer. The early DJI drones showed a lot of promise. However, they remained rather pricey and really targeted enthusiasts. I think they’re cool, but more in a casual hey, these are kind of neat and I wouldn’t mind playing with one once in a while way than anything serious. So, I set off to see if I could satisfy my curiosity without breaking the bank. This was back in the winter of 2016.

My drone requirements

I decided that what I wanted out of a drone was pretty minimal:

• Fly it inside of my house (ok, I admit this has limited application, but it would still be cool to have it follow me around and up-and-down stairs!)
• Fly it on my private property, below the tree line
• Fly it on private property where I’ve been authorized to fly it (relatives, friends, etc.), again below the tree line

That’s it. I didn’t really have any aspirations to fly a drone in other scenarios, especially knowing how quickly the regulations were evolving around drones. After poking around drone forums I learned of a company out of China called ZeroZero that had just started a Kickstarter campaign to produce the second generation of their Hover drone:

On May 31st 2016 I backed the project on Kickstarter. That began years or anticipation, disappointment, and general waiting. I checked in once in a while but the project never seems to get closer to shipping. When I finally got the notice that my order was ready, I had almost forgotten that I even backed it. In any case, in Summer 2020 my order was placed and the drone was on its way from somewhere in China. I received the drone in October 2020.

From the period of backing the Hover 2 Kickstarter campaign to when I actually had the drone in-hand, regulations around private drones continued to rapidly change and evolve. I wasn’t sure what to expect and I didn’t know how regulations were being applied to consumer drone technology providers. Throughout the period from 2016 through 2020 I had been assuming that regulations were outlining policy and guidance, not necessarily required technical controls. To my surprise, and almost immediate disappointment, I was greeted with this message when I turned the drone on for the first time:

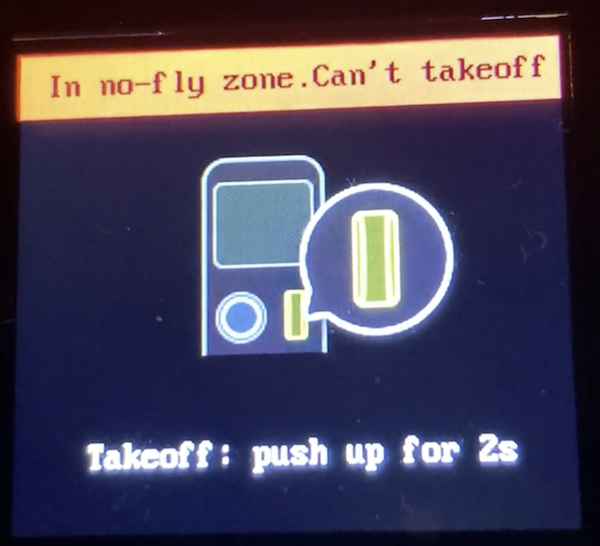
I took a short video as well when I tried to launch the drone in my home office.

Let’s see. So I bought a piece of hardware I’m not even allowed to use within my own house. That didn’t seem fair.

The rest of this article shows how I went about (1) figuring out how the drone’s geofencing technology worked and (2) how I was able to bypass it.

Ok, now that that’s out of the way, let’s continue.

Step 1: Figure out how the drone is geofencing

I’ve know that ADIZ zones exist, but I wasn’t actually aware of how large the one that covers the Washington DC metropolitan area was. I live in the ‘burbs of Washington DC and quite a way away from any significant landmark. Therefore I was pretty surprised when my shiny new drone said I was within a no-fly zone. I quickly discovered that I was indeed within this zone, thanks to a map that drone-maker DJI maintains:

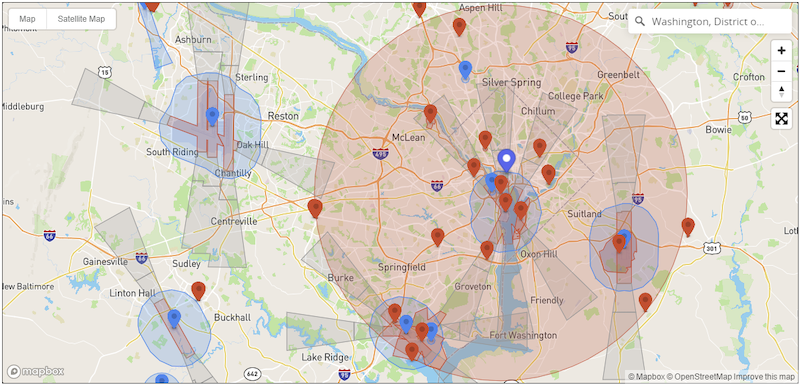
I’m barely within the large red circle (probably a mile or less). The drone obviously has GPS, and it was apparently able to get a strong enough GPS signal fix inside of my house. It must have been comparing its GPS coordinates to a pre-programmed database of no fly zones. Outcome: no flying for me.

The task now was to figure out what technology was being used to implement the geofencing. I started by looking in the most obvious place: the drones firmware. I was 99% sure the drone was running Linux, because let’s be serious, everything runs embedded Linux. I started by looking at the software that came with the drone. It was called FlyKit and looked like a pretty bloated Electron app. I quickly found the installation directory on my Windows box and that lead to log files. The log files were organized by date. Looking at the first log file gave a hint to the name and location of the firmware:

[2020-10-17 14:18:15.490] [info] {
  status: 200,
  message: 'success',
  meta: {
    version_no: '1.1.436-release10',
    url: 'http://firmware.cdn.gethover.com/release/hover2/1.1.436-release10/36e2257fe074dbcc26932a92c6156f7b/hover2.ota',
    checksum: '36e2257fe074dbcc26932a92c6156f7b',
    changelog_content: [ [Object], [Object] ],
    changelog_dialect: [ [Object], [Object] ],
    updated_at: '2020-08-21 16:32:00',
    minimum_version_requirements: { hover2: '1.1.379-release6' }
  }
}

I now knew I was looking for a firmware file called hover2.ota. I found a cached firmware file that has been downloaded and quickly confirmed that it was indeed a tarball of Linux software:

$ file hover2.ota
hover2.ota: gzip compressed data, last modified: Fri Aug 21 03:47:20 2020, from Unix
$ tar tvfz hover2.ota
-rw-rw-r-- zz/zz        738296 2020-07-31 01:54 ./ar8020.bin
-rw-r--r-- zz/zz        149704 2020-07-02 06:11 ./gimbal.img
-rw-rw-r-- zz/zz           192 2020-08-20 23:47 ./package.md5sum
-rw-r--r-- zz/zz         55276 2020-08-19 22:48 ./sonar.img
-rw-r--r-- zz/zz     409375836 2020-08-20 22:58 ./update_ext4.zip
-rw-rw-r-- zz/zz             8 2020-08-20 23:47 ./version

ext4 is the current default Linux file system, and since it was also the largest file, that seemed like the place to start. After extracting this file, I took a look at its contents:

$ 7z l update_ext4.zip
[ ... snip ... ]
   Date      Time    Attr         Size   Compressed  Name
------------------- ----- ------------ ------------  ------------------------
2008-12-31 12:00:00 .....     10414080     10046910  boot.img
2020-07-21 00:57:34 D....            0            0  META-INF
2020-07-21 00:57:34 D....            0            0  META-INF\com
2020-07-21 00:57:34 D....            0            0  META-INF\com\google
2020-08-20 22:57:47 D....            0            0  META-INF\com\google\android
2008-12-31 12:00:00 .....       132944        66353  META-INF\com\google\android\update-binary
2020-08-20 22:57:47 .....        80056        10172  META-INF\com\google\android\updater-script

Ah, I guess this drone runs some type of Android-based Linux distribution. Neat. The files under system appeared to be part of the base operating system. A few of them were clearly interesting:

2020-07-21 00:56:04 .....          943          231  system\etc\shadow
2020-07-21 00:56:04 .....          655          301  system\etc\gshadow
2020-07-21 00:56:04 .....         1381          548  system\etc\passwd

I filed these away, knowing they could be useful when I actually wanted to make changes to the drone’s operating state. Anyway, I continued looking for the geofencing software. Searching for files with ‘geo’ in them seemed as good an approach as any:

$ find . -name "*geo*"
./system/home/root/application/1.1.436/Captain/initdata/geo.data
./system/usr/lib64/libgeofence.la
./system/usr/lib64/libgeofence.so.1.0.0
./system/usr/lib64/pkgconfig/location-geofence.pc

Now I was on to something. I review the pkgconfig to see what I could learn about this software:

$ cat ./system/usr/lib64/pkgconfig/location-geofence.pc
prefix=/usr
exec_prefix=/usr
libdir=/usr/lib64
includedir=/usr/include

Name: location-geofence
Description: QTI GPS Geofence
Version: @VERSION
Libs: -L${libdir} -lgeofence
Cflags: -I${includedir}/location-geofence

This is what I was looking for. A quick Google for QTI GPS Geofence lead me to this link at usermanual.wiki. Apparently QTI is Qualcomm Technologies, Inc. and this is a software package/library that they offer for Android. Ok, now the software used to geofence was pretty clear but where were the data files? Those had to be in the firmware image somewhere. The first hit from my search for ‘geo’ provided that answer: [...]/Captain/initdata/geo.data. It appeared as though Captain was the name of the software that uses the geofence library from Qualcomm. I confirmed that there was a Linux executable called Captain within the firmware image:

$ file system/home/root/application/1.1.436/Captain/Captain
system/home/root/application/1.1.436/Captain/Captain: ELF 64-bit LSB executable, ARM aarch64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-aarch64.so.1, for GNU/Linux 3.14.0, BuildID[sha1]=3d86b839ca177f448f4fbff4e77644adb497c9b1, stripped, with debug_info

The directory where the geo.data file was found contained a number of data files. All of the files were in the format of [country-code]_[version]. It was logical that the countries with the most geofence data were the largest files. Here’s a selection of them including Brazil (BR), Canada (CA), China (CN), Germany (DE), England (GB), and the United States (US):

-rwxrwx---+ 1 None   269639 Aug 20  2020 BR_1.0.1
-rwxrwx---+ 1 None   477041 Aug 20  2020 CA_1.0.1
-rwxrwx---+ 1 None   164756 Aug 20  2020 CN_1.0.1
-rwxrwx---+ 1 None   678813 Aug 20  2020 DE_1.0.1
-rwxrwx---+ 1 None   486990 Aug 20  2020 GB_1.0.1
-rwxrwx---+ 1 None  5918849 Aug 20  2020 US_1.0.1

(The US file was an order of magnitude larger than the next biggest file).

The file was a blob, but it did contain some blocks of text:

$ strings -n 15 system/home/root/application/1.1.436/Captain/initdata/US_1.0.1 | head -15
Warner-Robins AFB-Installation
SAIPAN CORRECTIONAL FACILITY
GUAM WOMEN'S FACILITY
 GUAM YOUTH CORRECTIONAL FACILITY
-Grand Coulee Dam 2
 -Boston National Historical Park
-Idaho National Laboratory
-Independence Mall
Ellsworth-Installation 3
-Grand Coulee Dam 1
Ellsworth-Installation 1
 GUAM ADULT CORRECTIONAL FACILITY
HAGATNA DETENTION FACILITY
Ellsworth-Installation 2
!-Mount Rushmore National Monument

These were clearly places a drone shouldn’t be flown. The next logical step would have been to really understand the format of these files and write a proper parser (or figure out how to leverage the existing library). However, I had a hunch that that wouldn’t actually be necessary.

Step 2: Figure out how to bypass the geofencing

Now that I identified the software (Captain), library (libgeofence), and data file (US_1.0.1), the next step was to see if I could bypass the restrictions. To truly understand how the combination of these three components were used, I’d have to do a lot more digging. However, I figured I’d start with the most obvious ways to bypass geofencing first:

1. Could I simply remove US_1.0.1 from the data directory? What would happen if the file wasn’t found?
2. If US_1.0.1 is required, could I replace it with a zero-length file?
3. If US_1.0.1 is required, and it must be a properly formatted file, could I replace it with a file from another country?

In order to test any of these theories, I had to make modifications to the drone. I basically had two options:

1. Modify the firmware and try to load the modified firmware onto the drone
2. Modify the existing firmware on the drone while it was powered on/operating

Option (1) seemed like a lot of work. Also, the goal wasn’t to permanently modify the drone - it was to see if I could temporary bypass the geofence so I could operate the drone inside of my house. Therefore, I decided to start with option (2).

To get access to the drone, I had two connectivity mechanisms to try to get OS-level access:

1. The Wifi network that the drone creates for remote control by iOS/Android phone apps
2. The USB-C cable that is used for firmware upgrades

For (1), I could see from the files in the firmware that logging in via SSH would likely be possible. The sshd_config file in .../system/etc/ssh/ contained:

PermitRootLogin yes
PasswordAuthentication yes

I could also see that SSH was being explicitly allowed in SELinux policy from a boot script at .../system/etc/initscripts/init_post_boot:

#making ssh to login as admin
setsebool -P ssh_sysadm_login 1

So, with a valid root password, it was highly likely that I could SSH right into the drone while it was powered on. As I noted above, password files were in the firmware image and they appeared to contain a valid hash for the root account. Before I bothered trying to recover the root password, I poked around a little more. What I found was an easier solution staring me in the face. Buried a little further in the first log file I looked at was an interesting entry:

[2020-10-17 22:12:56.652] [info] {
  constructor: 'Error',
  killed: false,
  code: 1,
  signal: null,
  cmd: '"C:\\Program Files\\FlyKit\\resources\\auxiliary-packge\\platform-tools-win\\adb" -s G000H4045481012C shell "cat /etc/fw_version"',
  stack: 'Error: Command failed: "C:\\Program Files\\FlyKit\\resources\\auxiliary-packge\\platform-tools-win\\adb" -s G000H4045481012C shell "cat /etc/fw_version"\n' +
    'adb.exe: device unauthorized.\r\n' +
    "This adb server's $ADB_VENDOR_KEYS is not set\r\n" +
    "Try 'adb kill-server' if that seems wrong.\r\n" +
    'Otherwise check for a confirmation dialog on your device.\r\n' +
    '\n' +
    '    at ChildProcess.exithandler (child_process.js:308:12)\n' +
    '    at ChildProcess.emit (events.js:203:13)\n' +
    '    at maybeClose (internal/child_process.js:1021:16)\n' +
    '    at Process.ChildProcess._handle.onexit (internal/child_process.js:283:5)'
}

Apparently the FlyKit software attempts to check the version of the firmware on the drone when it starts. This is done by using adb, the Android Debug Bridge, to run a shell command on the drone. Specifically, the command is cat /etc/fw_version - a simple check to see the current firmware on the drone. The error message above was actually a bit misleading. I had another Android device plugged into my Windows computer (an Amazon Fire tablet) while I was first working with the drone and the FlyKit software assumed it was a drone and tried to check its firmware, hence the error message.

Now that I knew how to run the adb command, I plugged in the drone via its USB-C port and found the proper adb target:

$ ./adb.exe devices -l
* daemon not running; starting now at tcp:5037
* daemon started successfully
List of devices attached
$ ./adb.exe devices -l
List of devices attached
99968e2c               device product:apq8096-drone transport_id:1

After that, obtaining a root shell via USB was very straightforward:

$ ./adb.exe -s 99968e2c shell '/bin/sh'
/ # whoami
whoami
root

I poked around a little more to see what I could learn about the drone’s hardware and operating system:

/ # uname -a
uname -a
Linux apq8096 3.18.71-perf #1 SMP PREEMPT Tue Jul 21 12:39:13 CST 2020 aarch64 GNU/Linux

No surprise, an ARM-based system board. The kernel boot messages (via dmesg) gave a little more info:

[    0.000000] Linux version 3.18.71-perf (jenkins@zerozero-Name) (gcc version 4.9.3 (GCC) ) #1 SMP PREEMPT Tue Jul 21 12:39:13 CST 2020
[    0.000000] Boot CPU: AArch64 Processor [511f2112]
[    0.000000] Machine: Qualcomm Technologies, Inc. APQ8096v3 + PM8996&PMI8996 Drone

A Qualcomm processor for embedded devices:

The Qualcomm® APQ8096SG application processor features leading-edge premium mobile technology for powering next-generation devices, while supporting the ultimate in performance and power efficiency, ideal for small form factors and a wide variety of innovative and intelligent IoT applications.

The kernel boot messages also contained this warning, which I found amusing:

[    0.000000] **********************************************************
[    0.000000] **   NOTICE NOTICE NOTICE NOTICE NOTICE NOTICE NOTICE   **
[    0.000000] **                                                      **
[    0.000000] ** trace_printk() being used. Allocating extra memory.  **
[    0.000000] **                                                      **
[    0.000000] ** This means that this is a DEBUG kernel and it is     **
[    0.000000] ** unsafe for produciton use.                           **
[    0.000000] **                                                      **
[    0.000000] ** If you see this message and you are not debugging    **
[    0.000000] ** the kernel, report this immediately to your vendor!  **
[    0.000000] **                                                      **
[    0.000000] **   NOTICE NOTICE NOTICE NOTICE NOTICE NOTICE NOTICE   **
[    0.000000] **********************************************************

Apparently the drone maker was distributing a development kernel with their production drones. This is slightly interesting because of the typo of produciton above. The warning message (and corresponding typo) was introduced in May of 2014 and the typo was corrected in the fall of 2014. That gives a sense of the vintage of this Linux kernel.

Now that I was logged in to the drone interactively I simply had to test one of my theories listed above. After pondering, I decided that (3) was the best logical choice — replacing US_1.0.1 with another properly formatted file. This option obviated problems related to file-not-found or improperly-formated-data. I chose one of the smallest and most benign data files I could think of to use as the replacement: AQ_1.0.1 (Antartica). It was only 818 bytes in length.

I swapped the file, logged out, shutdown the drone, disconnected the USB-C cable, and then fired it back up.

Success

I was able to launch the drone from the floor in my home office. Here’s a short video showing takeoff and flight in my office.

While I ultimately used a USB connection to modify the drone, I was able to recover the root password and confirmed that I could SSH in to it while connected to its advertised Wifi SSID.

Endnotes

This was a fun exercise in exploring an embedded device. There are some legitimate reasons to want to bypass a drone’s geofencing. Restricting the use of a drone indoors and on private property doesn’t seem to be in the spirit of the geofencing enforcement.

Since I received the drone about a year ago and conducted most of this analysis it has remained in the closet in my office. I restored its original firmware and I’ve used it a few times. I got what I paid for in this drone: it’s an OK drone but there are much better ones out there. It’s been fun to fly at friends’ and relatives’ houses and has operated satisfactorily in general. The drone’s object avoidance is rudimentary and this seems to be an area that has been rapidly improving with newer drones. Perhaps my interest in drones will be renewed in the future as their technology continues to advance.